『邪馬一国の証明』　へ
『邪馬壹国の論理』へ

第一章　さらば「邪馬台国」よ　『よみがえる九州王朝』　へ
第二章　I 短里論争

あとがきにかえて・解説にかえて

魏志倭人伝と短里　『周髀算経しゆうひさんけい』の里単位

あとがきにかえて

古田武彦

　この数年間、日本の古代史学界は「邪馬台国」問題から“目をそむけて”きつづけたように見える。けれども、学問そのものは一歩も停滞しなかった。
　それどころか、研究史上、一つの画期をなす論文が出現した。谷本茂氏の「中国最古の天文算術書『周髀算経しゅうひさんけい』之事」（「数理科学」一九七八年三月）がこれである。
　『周髀算経』は、周代に生れ、後漢末（二〇六〜二二〇）に成立した本だ。冒頭は周公と商高（殷人）との対話にはじまる。このようなスタイルは、通例（後代の啓蒙主義史観からは）“周公に仮託した後代の偽作”と見なされることが多い。ところが、そこに語られた星の運行は、まさに紀元前一一二二（前後一〇〇）年頃のものであることが判明したのである（能田忠亮『周髀算経の研究』）。文字通り殷末・周初の、周公の頃だ。さらに、後に増拡された記事の部分には、春秋末から戦国初にかけて出現した、星の運行が記されている。すなわち、この記事の、この時期に成立したことが認められるのである（同右）。
　以上によって、この『周髀算経』が周初から周の中・後期にかけて“生育”していった、という性格の内容をもつことが明らかとなった。そして同時に、注記を加えて編成された時期もまた、これを確定できるのである。なぜなら、編者たる趙君卿（漢）によって付せられた注は、もっとも新しいものとして「二〇六」成立の引用書をふくんでいる。従ってこれ以後の成立だ。また編者は「漢」の人物であるから、「二二〇（漢の滅亡）」と以前に属する。すなわち上限「二〇六」、下限「二二〇」の間、十四年間のうちに、この書は編成されたのである。この後漢末十四年間は、まさに『三国志』の第一巻の時期、つまり曹操の活躍していた、そのさ中である。
　さて、若き自然科学研究者、谷本氏の発見は、この『周髀算経』の中で用いられている里単位が計算によって確認できる、という一点にあった。それは「一里＝約七六〜七メートル」だった。これはわたしがかつて『「邪馬台国」はなかった』でしめした魏晋（西晋）朝短里（一里＝約七五メートル。精しくは「七五〜九〇メートル」の間で、七五メートルに近い、とした）と驚くべき一致をしめしたのである。氏はこの両者の一致を「単なる偶然の一致」としてすませることは出来ない」と結ばれた。
　思えば、わたしにとって氏との邂逅（かいこう）は、楽しき思い出にみたされている。当時京大の工学部の学生であった氏は、わたしに一葉の書便をもたらされた。その中で、わたしの本に着目したのは、一に「学問としての方法」にあることを、懇切にのべておられたのである。
　爾来、氏はわたしの家にしばしば訪れられ、わたしもこの若き探究者に最近の発見を告げることを楽しみとするようになった。そのある目（一九七五年）、氏は“『周髀算経』が「短里」で書かれている”という、自己の発見を告げられたのであった。わたしの家の夕食の席でしめされた一片の計算用紙、それが今もわたしの手もとになつかしく保存されている。
　その後、東京に行かれた氏は、右の発見を次々と発表された。まず「東アジアの古代文化」文献の会、次いで右の「数理科学」である。
　この論文によってもたらされたもの、その第一は白鳥庫吉以来、最近の山尾幸久・松本清張氏等に至る、「倭人伝里数値誇張説」の否定である。なぜなら魏使や帯方郡官僚などの「誇張」というような“恣意”の結果なら、“全く別々の二書（『周髀算経』と『三国志』）において、同一の里単位が現われる”そのようなことはありえないからである。
　従って“『三国志』において「短里」が使われている”この事実は動かしがたい。いかに古代史学界がこの発見に“無関心”をよそおいつづけようと、結局、事実は頑固にして動かしがたい、のである。
　その第二は、倭人伝の「一万二千余里」（帯方郡治→女王国）が「短里」という実定値で書かれている、とすれば、あの「邪馬台国」近畿説がもはや成り立ちえないことは、自明だ。なぜなら従来の近畿説は、この里程記事を誇張として「無視」ないし「軽視」するところに成り立っていたからである。
　さらに、「誇張」等の名に乗じて、「部分里程」の総和が「全里程」（一万二千余里）にならぬまま放置して、その上に立論してきた、従来のすべての「邪馬台国」論者も、今や鼎（かなえ）の軽重を問われるに至ったのである。
　その第三は、卑弥呼の墓だ。「径百余歩」と書かれた、その長さは、「一里＝三百歩」（『周髀算経』等）であるから、「三〇〜三五メートル」の円冢（＝塚）となる。従って「一五〇〜二〇〇メートル」の前方後円墳（たとえば箸墓）などにあててきた、従来の知見は当然否定されざるをえない。
　このように、「短里」問題を契機として、邪馬一国研究史は画期をむかえた。後代、忘るべからざる必須文献となるであろう、この谷本論文を、氏の御快諾をえてここに収載させていただくことを喜びとする。現代の若き探究者が独創的に、未来の広大な研究の基礎を築いた、これこそその明らかな証跡となるものであろうから。

解説にかえて
　　　魏志倭人伝と短里 -- 『周髀算経しゆうひさんけい』の里単位

谷本茂

　歴史書の中に現われる度量衡（どりょうこう）のいろいろな単位が、現在のメートル法で表わして正確にどのくらいかを調べることは、ただ昔の単位の実態を知るという知的興味に留まらず、歴史書に記述された内容を定量的に把握し、史料の真実性の批判検討を通して歴史の実相に迫るという意味からも、重要なことである。小泉袈裟勝（こいずみはさかつ）氏の一連の著作（『度量衡の歴史』『歴史の中の単位』など）からも知られるように、東洋の度量衡単位の変遷に関して、先学の研究により多くのことが解明されてきたとはいえ、いまだ明らかでない点も残されている。
　特に、「里（り）」という単位は不思議である。「一里塚」などという場合の目本の一里は、三十六町で約四キロメートルである。同じ「里」でも、現代中国においては五百メートルである。歴代中国の里単位は、時代によって多少の変化はあるものの、一里は約四百ないし五百メートル程度であり大差はないとされていた（詳細は『角川漢和中辞典』付録「中国度量衡の単位とその変遷」などを参照のこと）。日本の度量衡単位は中国のものとそれ程ひどい違いは無いのが普通であるのに、この里だけは一桁異っているのである。いつどうしてこんなに違ってしまったのか、その由来はあまりはっきりしていない。
　ところが、中国においても、通常知られている里とは大幅に異る短い里が存在していたことが分かってきた。『周髀算経』という中国古代の天文算術書の中に現われる「一里」は約七十六ないし七十七メートル程度である（拙著「中国最古の天文算術書『周髀算経』之事」『数理科学』一九七八年三月号）。
　有名な「魏志倭人伝」の中の里は、通常の里単位認識では到底理解できない。これを、誇大値の類とせず、従来知られていた里とは異る「短い里」として理解されたのが、安本美典氏、野津清氏、古田武彦氏などであった。特に、古田氏は、『「邪馬台国」はなかった』その他の著作で「魏晋（西晋）朝短里」という概念を提出された。それによれば、一（短）里は約七十五ないし九十メートルであり、しかも七十五メートルに近い数値であるという。『周髀算経』の里と古田氏の提示された短里とは、数値がきわめて近く、単なる偶然の一致とみなすことはできないであろう。
　「短里」の存在が明らかになってきたので、『三国志』に留まらず、他の古代文献の史料批判に対しても影響を及ぼすことが予想される。『三国志』に関しては「全面短里」か「部分短里」かの論争がある。また、既に古田氏が指摘されたごとく、『華陽国志』『戦国策』『文選』などの史料中にも短里ではないかと思われる里数値が現われている。今後の史料研究によって短里の実態が更に明らかにされることを期待したい。
　私は学生時代に加藤平左ヱ門氏の『日本数学史』を読んでいて『周髀算経』という書物を知った。その時、古田氏の提示されていた短里の事が頭に残っていたので、注意を引かれて計算してみたのである。従来の説から一寸千里の法をみれば、古代人の愚しさに映るであろうが、その内谷を真面目に検討することにより短里と巡り合うことができたと言えるであろう。私にとってこのささやかな経験は、古田氏が力説される「史料批判の重要性」を実感するに充分であった。
　史料批判を慎重に行なうということは、従来の定説に依拠して史料を見る（読む）のではなく、その史料自らの語るところを真剣に検討し、その結果を従来の定説と実証的に比較検討するといつ手続きである。これは史料に基づく歴史研究の常識であろう。しかし、古代史研究の分野においては、この常識が充分吟味されているようには思えない。そういった意味で、あの稲荷山鉄剣銘文の一件では大いなる失望を抱いた。
　「史料批判とはその根底において、その史料をあつかう自己自身への批判でなければならぬ」と言い切る古田氏は、その立場で実践的に古代史料に取り組み、前人未踏の日本古代史像を得つつある。『「邪馬台国」はなかった』以降の一連の氏の著作の結論は、旧説に馴染んできた人々には、非常識とも奇をてらうものとも映るかも知れない。それ故、個々の論点について種々の議論か起こるのも当然であろう。旧説にとらわれず、自由な立場からの実りある論争を期待したい。
　的確な批判を経た史料に依拠する立場からのみ、古田氏の所論を真に乗り越え、古代史研究を先展させることが可能であるように思われる。
　『周髀算経』は周の時代（西周はBC一〇五〇年〜BC七七一年）に行なわれた天文観測の方法を記載する中国最古の天文算術書であるといわれている。
　中国の古代の算術書は、いわゆる算経十書として版本が伝わっており、その中でも、『周髀算経』『九章算術』『海島算経』などは漢から三国時代（二〜三世紀）にかけて整理され、教科書として使用されていた模様であるから、中国古代の算術知識を知る上で興味深いと言えよう。
　『周髀算経』という書物の成立時期は、だいたい三世紀初め頃と思われる。初めて注釈した趙君卿（ちょうくんけい）という人が、「漢」の趙君卿と記しており、その注に引用されている書物のなかで後漢の劉洪（りゅうこう）の作といわれる『乾象歴けんしょうれき』（二〇六年頃）が最も新しいことから、趙君卿が注釈整理したのは、二〇六年から二二〇年（後漢末）の間の時期ということが分かる。『漢書』芸文志には『周髀算経』の名は見られないので、前漢以前には現存のような形では知られていなかったようである。
　『周髀算経』の本文は、同時代のことから後漢時代の暦にまで言及している。明らかに同一時代に同一人の手に依って成立したとは思われない文面があり、多くの部分で趙君卿自ら、これらは周髀の本文にあらずと注記しているのである。
　そして、天文学の立場から『周髀算経』の詳細な史料批判を行なわれた能田忠亮氏（『周髀算経の研究』）によれば、天文学的にみて、BC十二世紀前後百年ばかりの間においてのみ観測しえる天象や、春秋時代中期以降戦国時代初期の間（ BC六世紀〜BC五世紀）に起源をもつとみられる内容のものがある反面、後世後漢時代の知識も多分に含まれているという。
　要するに、『周髀算経』の成立に関しては、この書に見える概念や方法の起源は相当古く、周時代以来伝承されてきた種々の天文算術知識を集成して、後漢末頃に、最初の注釈者趙君卿により現存のような形に整理されたとみて大過ないであろう。
　『周髀算経』上下二巻の中には、諸説を寄せ集めたため、上巻と下巻とで首尾一貫しない記述も幾つか見られる。たとえば、上巻では地は平坦だと考えているのに対して、下巻では、天は笠（かさ）に似ており地は裏返したタライ（盥）の形をしているという有名な蓋天（がいてん）説が登場する。ここには、漢時代の渾天（こんてん）説と蓋天説との論争が一部反映しているとみることができよう。『周髀算経』の全貌は、近々全訳が刊行されるとのことであるから、興味ある読者はそちらを参考にされたい（科学の名著シリーズ『中国天文学・数学集』朝日出版社刊）。また、天文観測事例については前掲の能田氏の詳細な専門的研究がある。
　ここでは、里単位に関連して、『周髀算経』の中の天文観測（測量術）の基本的方法についてのみ述べることにする。
　『周髀算経』は、周公（周の武王の弟）と商高（当時の賢大夫）の問答から始まる。ここでは天文観測の方法の基礎が、勾股弦（こうこげん）の法、用矩（ようく）の法として述べられており、内容的には原始的な三角測量の原理と簡単なピタゴラスの定理の応用である。
　直角三角形の直角を挾む二辺を勾（句とも記す）、股といい、斜辺を弦と呼ぶ。三対四対五の率は、「自然の率」として非常に古くから知られていたようである。なお、本書では、二辺が既知の場合に他の一辺を開平により求める一般的なピタゴラスの定理の応用も見られる。用矩の法とは、直角三角形の相似関係により、距離・高さ・深さなどを求める方法で、原始的な三角測量法ということができよう。「矩」とは、その正確な形状は分からないが、さしがねの様な形をした測量具である（図１参照）。

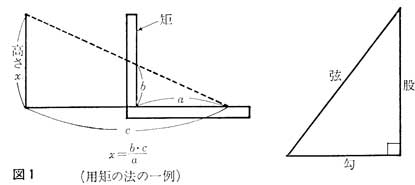
　書名の「周髀」の由来であるが、髀は八尺の棒のことで、周代に天子がこれを地面に垂直に立てて股とし、日影を勾として、各種の測量を行なったことに基づき、周髀と言われるようになったとある。
　周公と商高の問答に続いて、栄方と陳子の問答がある。栄方・陳子は周公の後代の人ではあるが、いつ頃の人かは定かでない。この部分では、測量の公理であるところの「一寸千里の法」が説明され、先述の勾股弦の法、用矩の法を実際に応用して、天地の大きさが具体的に求められている。
　周の地で夏至の日（南中時）に、地面に垂直に立てた八尺の周解の影の長さは一尺六寸である。南に千里の地においては影は一尺五寸、北に千里の地においては影は一尺七寸である。よって、八尺の股（周髀）に対する勾（影）の差一寸は、地上の距離にして千里に当たる。これが「一寸千里の法」である。現代の我々の知識からすれば何とも幼稚極まりないし、その方法の誤りも明らかであるが、ともかく、古代の中国人は、この一寸千里の法により天地の大きさを具体的に知ろうとしたのである。
　夏至の日には、八尺の周髀の影は一尺六寸であり、冬至の日には、影は一丈三尺五寸である（一丈＝十尺、一尺＝十寸）。よって、夏至の日に太陽は観測地より南一万六千里の地の真上にあり、冬至の日には、太陽は南十三万五千里の地の真上にあることになる。影の長さは南中時に測定し、地面は平坦であると考えている訳である。
　夏至以後、影は段々長くなり、丁度六尺となる時がある。この時、穴の直径一寸長さ八尺の竹筒をとって太陽を見れば、その穴と太陽がほぼ一致する。よって太陽の直径は、八尺先にある一寸の穴径の率から求められる。今、股八尺勾六尺であるから弦は十尺である。したがって一寸千里の法により、観測地から太陽の真下の地まで六万里、太陽の高さは八万里、観測地から斜めに十万里のかなたに太陽がある。太陽の直径は、十万里に八十分の一の率を乗ずることにより、千二百五十里と求められる（図2参照）。

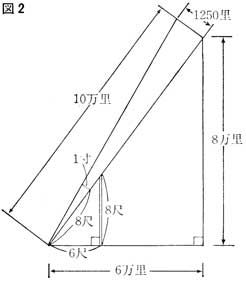
　八尺の周髀を立てて北極（北極星　ーー現在の北極星とは異り帝星であろう）を望むと、その勾は一丈三寸となる。よって周の地から北へ十万三千里行くと北極の真下に至る。
　以上の例のように、昼は太陽を、夜は星を利用して天地の大きさ及び方位を求めており、最終的に、地上で太陽の光の届く範囲は直径八十一万里（約六万二千キロメートル）であると記している。
　『周髀算経』の天文観測の数値は、実測値と机上の計算値が混在してはいるが、いずれにしても、一寸千里の法を公理的命題として、一貫して同じ里単位が使われている。幸いにも、一寸千里の法の根拠が挙げられていることにより、我々は一里が何メートルであるか正確に知ることができる。

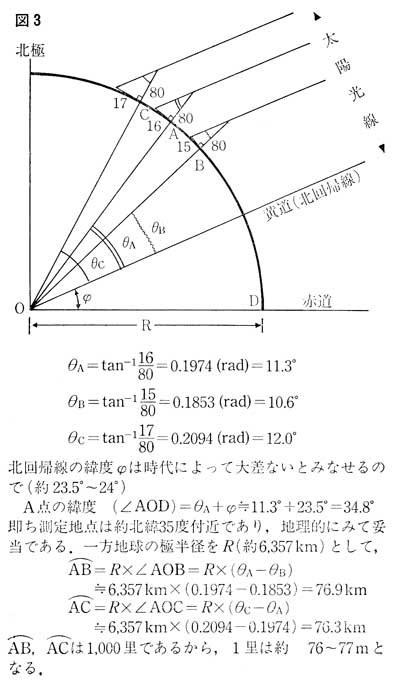
　南北に各々千里離れた三地点で夏至の日の影の長さが分かっているのであるから、三角法の簡単な計算により（図3参照）、観測地点は北緯約三十五度であり、一里は約七十六ないし七十七メートルと知ることができる。勿論観測の誤差などを考えれば、有効数字としては慎重に処理しなければならないにしても、従来知られていた約四百〜五百メートルの里とは明らかに異る里単位である点を確認することが重要である。

『古代の霧の中から』　へ

『邪馬壹国の論理』へ