大宝律令の中の九州王朝 泥憲和(会報68号)
『市民の古代』第5集の古田武彦講演「筑紫舞と九州王朝」中の 魏・西晋朝短里の三論証へ
闘論へ
『九章算術』の短里
『九章算術』の短里
姫路市 泥 憲和
はじめに
拙文を投稿するにあたって、同じアイデアをどなたかが既に発表しておられるかも知れないと気になり、数人の先輩方に尋ねてみました。すると「自分は気付かなかった。まあ、発表してみればいいんじゃないの?」とのことでした。このあたりの大らかさが「古田史学の会」の居心地の良いところです。また言われればすぐに乗ってしまうのが私の人間の軽いところであります。
そういう次第で投稿するに至ったのですが、もしも先のようなことがあれば、それは私の不明ということでご寛恕願いたいと存じます。
一、おさらい
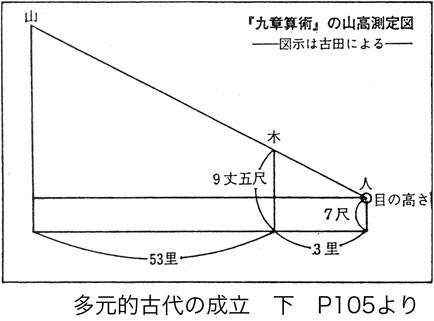
さて、ここに取り上げる『九章算術』資料は「九州王朝の証言」(『多元的古代の成立 下』P105)で紹介されています。短里の論証部分で、古田先生が安本美典氏に反論しながら自説を展開しておられる箇所です。思い出して貰うために、ちょっとおさらいしてみましょう。
『魏志』は天柱山の高さを「二十余里」と記しているところ、天柱山の実高は一八〇〇メートルですので、「二十余里」を「二十三〜四里」と見れば、一里七十五メートルの短里なら約一七二五メートル〜二一六〇メートル。ぴったり妥当します。しかし長里(安本氏は一里=四三四メートル説)なら、一万mを超えてしまう。こんな山が三国志の世界にあるはずがない。天柱山の高さは短里で書かれている。これが古田先生の論証です。
ところが安本氏から反論がありました。
“里程は標高ではなく頂上までの道のりである可能性がある”と。
古田先生はこれに対して、三国志には山中の道のりを表現する記述法がちゃんとあって、それは高さを表現する記述法と明らかに異なっている実例を幾つも示されます。
その上でさらに、当時の中国に山高を測る計算法が実際に存在していたことをも指摘されました。その例証として紹介されているのが、本投稿でテーマとする『九章算術』です。
二、九章算術を計算してみる
まず問題文と答を再掲します。
「山有り。木の西に居す。其の高さを知らず。山を去る五十三里。木の高さ九丈五尺。人、木の東三里に立ち、木末を望む。適(ちょうど)、山峯と斜平す。人目の高さ七尺。問う。山の高さ、幾何(いかん)。
答えて曰く、一百六十四丈九尺六寸太半寸。(太半寸は三分の二寸)
この計算は簡単です。(図参照)
(9.5−0.7)÷3×(53+3)+0.7=164.967
計算上、里数はただの比ですから、長里でも短里でも答えは同じになります。だから古田先生は『九章算術』の問題が短里で書かれているか長里かについては触れておられません。先生の意図はあくまでも山高を測定する計算法が三世紀に存在したことを示すにあったのですから、それで当然です。。
では実際の所、ここに書かれた里程は長里なのか短里なのか、私は興味を持ちました。
するとこの引用箇所が、実は短里でなければ理解し難いことに気付いたのです。
三、実測値に当てはめるとどうなるか・・・
メートル法に換算すれば、165丈の山は約396メートルになります。そこらへんにある、普通の里山ですね。木の高さは約22.8メートルです。(※1.)
次に距離。一里が434メートルの長里なら、人と山の距離は約24,304メートル。これは大阪〜神戸の直線距離に相当します。そして人から木までは約1,302メートル。(※2.)
すると大阪駅にいる人が高さ23メートルの木を1.3kmも離れた所から眺め(まあ見えないことはないでしょうが)、そのはるか向こう、24kmも離れた神戸市の、たった400メートル足らずの山の高さを測ろうとしていることになります。水平線の彼方に米粒ほどの大きさに見える山の高さを…。これはいくら架空の計算問題だとしても非現実的すぎるのではないでしょうか。
試みに仰角はいくらぐらいになるかを計算してみると、約0.9度でした(笑)。(※3.)
星の観測ではあるまいし、山の高さを測るのにどうしてわざわざこんな視角になる距離を選ぶ必要があるでしょうか。長里で考えると、全くこれは愚問であるとしか評せません。
では一里が75メートルの短里ではどうか。
山〜木は約3,975メートル。木〜人は約225メートル。山〜人は約4,200メートルです。
約4キロメートル先にある400メートルほどの山高を測るため、高さ約23メートルの木を約230メートル離れて観測する。
これはきわめて自然な出題ではないでしょうか。
この場合仰角は5.5度程度になりますから、簡単な測定器で計測可能です。
こうして、長里で解釈すると不自然なのに短里概念を導入すれば自然に理解できる例が、また一つ増えたわけです。
まとめ
短里を認めたくない人は、それでも納得しないでしょう。
「たしかに長里を当てはめれば不自然かも知れない。しかしこれは実際に測定する必要のない机上の計算問題なのだから、実感と齟齬があったっていいんだ。」
こんな風に言う人がいるかも知れませんね。そういう人には『九章算術』の中身を見て貰い、これはパズル好きの現代人に向けて書かれた本じゃないよと言うしかありません。
『九章算術』は次に示す章題を見ても判るとおり、極めて実用的な書なのです。
方田 ーー主に田畑の(年貢のための)面積計算と分数の計算。
粟米 ーー交換比率の異なる商品を物々交換するための計算。比例算。
衰分 ーー商品とお金との分配。比例按分。利息計算。
少広 ーー面積体積から辺の長さを求める。平方根や立方根。
商功 ーー土石の量などを求める土木計算。体積。
句股 ーー三平方の定理に関する問題。
他にはこんな問題がありますので、お好きな方は解いてみて下さい。
○ 豚2匹と牛3匹なら8両、豚3匹と牛2匹なら7両。問う、牛豚1匹の値は幾何。
(※)
※1.一尺が大体24センチ、一丈はその十倍にあたる2.4メートル。
山高は2.4×165=396メートル。木の高さは2.4×9.5=2.28メートル。
※2.木〜人、43×3=1,302メートル。
山〜人、434×56=24,304メートル
※3.目の高さ2.4×0.7=1.68≒1.7メートル。
tanθ=(23−1.7)÷434×3=0.016359
θ=約0.9度
_______________________________________
追加、泥氏の見解を支えるメールが来ました。ご一読下さい。(2007年1月15日掲載追加)
泥 憲和 様
古田史学会報 No.77泥 憲和 氏の『九章算術』の短里を拝見しました。
九章算術では短里が前提だという結論はその通りと思います。
さらに、だめ押しか(蛇足か?)思われることがあります。
それは、地球が球であるという影響が長里ではかなり大きい、ということです。
すなわち、長里では、この山の高さは24 km離れたところからは約45 m低く見えるのです。
自分関係のページで恐縮ですが、ここの(2)式で計算できます。
http://www.spu.ac.jp/kenshu/webkouza/webnaiyou/jinkoueisei1.htm
いくら昔の人でも 400 mの山の高さが、355 mに見えるというようなケースは
例として取り上げないのではないでしょうか。
これが短里の場合は、4.2 km離れたところから見るので山の高さの誤差は約1 mです。
400 mの山の高さの誤差が約1 m なら、今の人でも文句を言わないのではないかと思います。
柴村英道
これは会報の公開です。史料批判は、『新・古代学』(新泉社)・『古代に真実を求めて』(明石書店)が適当です。
新古代学の扉 インターネット事務局 E-mailはここから。Created & Maintaince by" Yukio Yokota"